前言

進入演算法介紹，行百里者半九十，真的是越接近結束寫文章的壓力越大...

主題

今天先介紹線性迴歸的演算法進行暖身，希望後面幾天可以一次多介紹幾種。

Linear Regression

線性迴歸演算法，從名稱來看，線性(Linear)代表這個模型的變數都是一次函數，迴歸(Regression)代表考慮針對連續的有理數目標。
具體而言，公式長的如下:

y:預測的目標值(Label\Target)，有理數
x:給定的input的資料
w:參數權重
公式用白話文就敘述就是，針對給定的資料(x0,x1,...)，用一組參數權重(w0,w1,...)進行加權相加後，得出對應的目標值(y)。

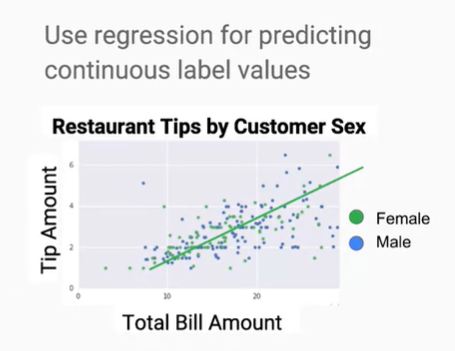
前面這樣有說和沒說一樣，從圖形上來看，就是用線性函數來擬合目標數值。
線性函數是什麼呢?單變數情況下就是一條線、雙變數就是一張平面、高維度就是超平面(hyper-plane)。
擬合是什麼概念呢?就是去模擬這些數值的趨勢，這些數值的分布會和函數的數值很相近。

接著，前面擬合說道資料與函數的數值很接近，如何定義很接近呢?沒錯，就是要使用到Evaluation的方法去度量。一般而言，迴歸問題中最普遍使用的就是 Mean Squared Error: 。
這樣就形成一道經典的最小平方法問題，這道問題是有公式解(closed form solution)的，也就是直接套公式就能得到最佳的W參數值。公式如下:

在一些好的性質下，只要對W進行微分就能簡單推導出來。
能夠一口氣直接得到W的確非常不錯，然而，當資料很大時此方法卻不怎麼管用，為什麼呢?
假設資料筆數為N筆，Gram matrix 的大小就會有 NxN 項 elements，當資料量增加方陣成長的速度指數上升非常快速，將導致記憶體無法有足夠空間一次儲存起來。除此之外，要計算反矩陣需要相當大的時間複雜度，資料量越大的時候，計算的時間也會花越久。
因此，當資料非常大時，只好捨去一步登天的方式，改用迭代更新的演算法進行最佳化，也就是梯度下降法\最陡梯度法(Gradient descent\Steepest desent)，之後會針對此演算法進行介紹。

到這邊稍微總結一下，利用番外篇提到的分解方式:
Represntation: Linear Regression Model
Evaluation: Mean Squared Error
Optimization: Closed Form\Gradient desent